K-Means

The code is based upon the Wikipedia description [wikikmeans]. The objective of the algorithm is to minimize the intra-cluster variance, given by

where 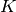is the total number of clusters, the set of points in the ‘th cluster, and the center of the ‘th cluster.

When k-means has minimized the intra-cluster variance, it might not have found the global minimum of variance. It is therefore a good idea to run the algorithm several times, and use the clustering result with the best intra-cluster variance. The intra-cluster variance can be obtained from the method find_intra_cluster_variance.

[wikikmeans]

http://en.wikipedia.org/w/index.php?title=K-means_algorithm&oldid=280702005

K-Means Example

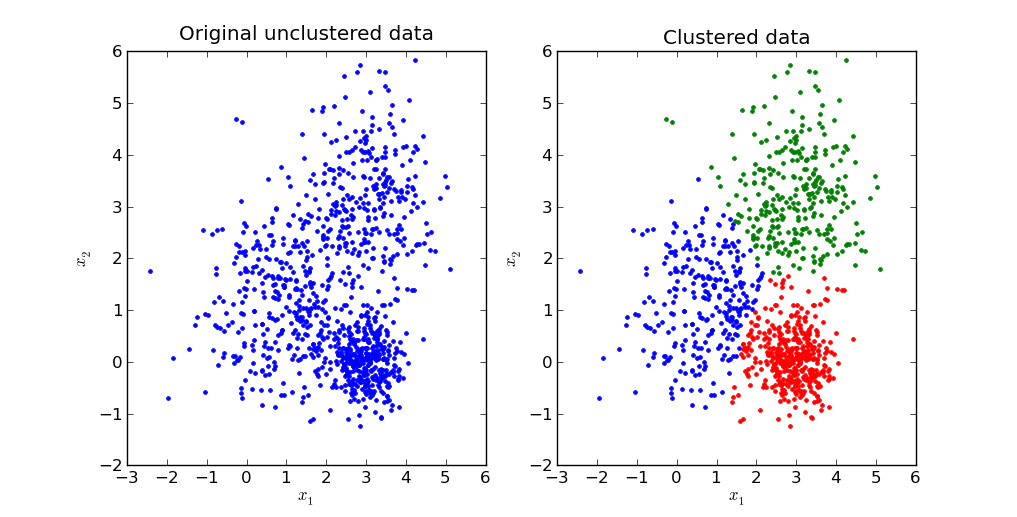
To demostrate the K-means algorithm, we will construct a simple example with three clusters with Gaussian distribution.

from matplotlib.pylab import *
from pypr.clustering.kmeans import *
from pypr.clustering.rnd_gauss_clusters import *

# Make three clusters:
centroids = [ array([1,1]), array([3,3]), array([3,0]) ]
ccov = [ array([[1,0],[0,1]]), array([[1,0],[0,1]]), \
          array([[0.2, 0],[0, 0.2]]) ]
X = rnd_gauss_clusters(centroids, ccov, 1000)

figure(figsize=(10,5))
subplot(121)
title('Original unclustered data')
plot(X[:,0], X[:,1], '.')
xlabel('$x_1$'); ylabel('$x_2$')

subplot(122)
title('Clustered data')
m, cc = kmeans(X, 3)
plot(X[m==0, 0], X[m==0, 1], 'r.')
plot(X[m==1, 0], X[m==1, 1], 'b.')
plot(X[m==2, 0], X[m==2, 1], 'g.')
xlabel('$x_1$'); ylabel('$x_2$')

The second plot of this example will give the clustering result from the algorithm.

Application Programming Interface

pypr.clustering.kmeans.find_centroids(X, K, m)

Find centroids based on sample cluster assignments.

Parameters :

X : KxD np array

K data samples with D dimensionallity

K : int

Number of clusters

m : 1d np array

cluster membership number, starts from zero

Returns :

cc : 2d np array

A set of K cluster centroids in an K x D array, where D is the number of dimensions. If a cluster isn’t assigned any points/samples, then it centroid will consist of NaN’s.

pypr.clustering.kmeans.find_distance(X, c)

Returns the euclidean distance for each sample to a cluster center

Parameters :

X : 2d np array

Samples are row wise, variables column wise

c : 1d np array or list

Cluster center

Returns :

dist : 2d np column array

Distances is returned as a column vector.

pypr.clustering.kmeans.find_intra_cluster_variance(X, m, cc)

Returns the intra-cluster variance.

Parameters :

X : 2d np array

Samples are row wise, variables column wise

m : list or 1d np array

Cluster membership number, starts from zero

cc : 2d np array

Cluster centers row-wise, variables column-wise

Returns :

dist : float

Intra cluster variance

pypr.clustering.kmeans.find_membership(X, cc)

Finds the closest cluster centroid for each sample, and returns cluster membership number.

Parameters :

X : 2d np array

Samples are row wise, variables column wise

cc : 2d np array

Cluster centers row-wise, variables column-wise

Returns :

m : 1d array

cluster membership number, starts from zero

pypr.clustering.kmeans.kmeans(X, K, iter=20, verbose=False, cluster_init='sample', delta_stop=None)

Cluster the samples in X using K-means into K clusters. The algorithm stops when no samples change cluster assignment in an itertaion. NOTE: You might need to change the default maximum number of of iterations iter, depending on the number of samples and clusters used.

Parameters :

X : KxD np array

K data samples with D dimensionallity.

K : int

Number of clusters.

iter : int, optional

Number of iterations to run the k-means algorithm for.

cluster_init : string, optional

Centroid initialization. The available options are: ‘sample’ and ‘box’. ‘sample’ selects random samples as initial centroids, and ‘box’ selects random values within the space bounded by a box containing all the samples.

delta_stop : float, optional

Use delta_stop to stop the algorithm early. If the change in all variables in all centroids is changed less than delta_stop then the algorithm stops.

verbose : bool, optional

Make it talk back.

Returns :

m : 1d np array

cluster membership number, starts from zero.

cc : 2d np array

A set of K cluster centroids in an K x D array, where D is the number of dimensions. If a cluster isn’t assigned any points/samples, then it centroid will consist of NaN’s.