Gaussian Mixture Models¶
A multivariate normal distribution or multivariate Gaussian distribution is a generalization of the one-dimensional Gaussian distribution into muliple dimensions.

The distribution is given by its mean,  , and covariance,
, and covariance,  , matrices.
To generate samples from the multivariate normal distribution under python, one could use the
numpy.random.multivariate_normal function from numpy.
, matrices.
To generate samples from the multivariate normal distribution under python, one could use the
numpy.random.multivariate_normal function from numpy.
In statistics, a mixture model is a probabilistic model for density estimation using a mixture distribution. A mixture model can be regarded as a type of unsupervised learning or clustering [wikimixmodel]. Mixture models provide a method of describing more complex propability distributions, by combining several probability distributions. Mixture models can also be used to cluster data.
The Gaussian mixture distribution is given by the following equation [bishop2006]:

Here we have a linear mixture of Gaussian density functions,  .
The parameters
.
The parameters  are called mixing coefficients, which must fulfill
are called mixing coefficients, which must fulfill

and given  we also have that
we also have that

Sampling and Probability Density Function¶
PyPR has some simple support for sampling from Gaussian Mixture Models.
Gaussian Mixture Models
- pypr.clustering.gmm.sample_gaussian_mixture(centroids, ccov, mc=None, samples=1)¶
Draw samples from a Mixture of Gaussians (MoG)
Parameters : centroids : list
List of cluster centers - [ [x1,y1,..],..,[xN, yN,..] ]
ccov : list
List of cluster co-variances DxD matrices
mc : list
- Mixing cofficients for each cluster (must sum to one)
by default equal for each cluster.
Returns : X : 2d np array
A matrix with samples rows, and input dimension columns.
Examples
from pypr.clustering import * from numpy import * centroids=[array([10,10])] ccov=[array([[1,0],[0,1]])] samples = 10 gmm.sample_gaussian_mixture(centroids, ccov, samples=samples)
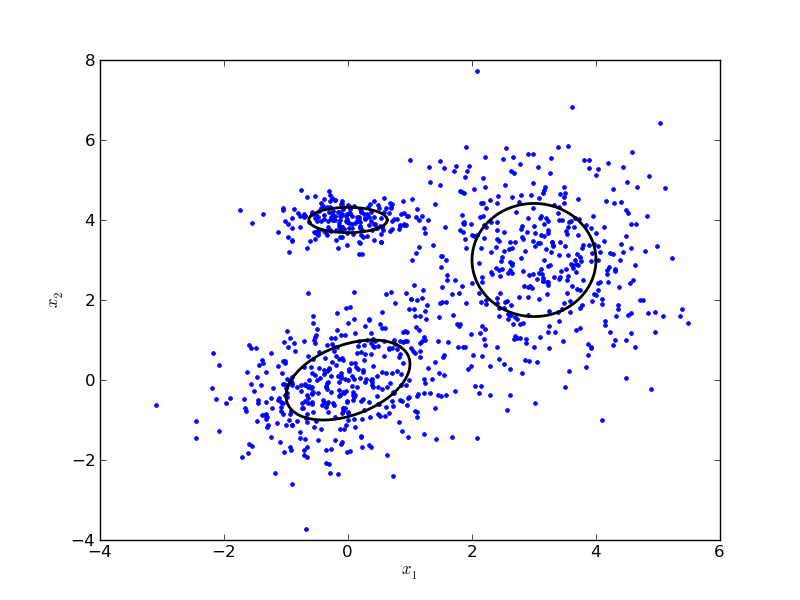
The example sample_gmm gives an example of drawing samples from a mixture of three clusters, and plotting the result.
# Drawing samples from a Gaussian Mixture Model
from numpy import *
from matplotlib.pylab import *
import pypr.clustering.gmm as gmm
mc = [0.4, 0.4, 0.2] # Mixing coefficients
centroids = [ array([0,0]), array([3,3]), array([0,4]) ]
ccov = [ array([[1,0.4],[0.4,1]]), diag((1,2)), diag((0.4,0.1)) ]
# Covariance matrices
X = gmm.sample_gaussian_mixture(centroids, ccov, mc, samples=1000)
plot(X[:,0], X[:,1], '.')
for i in range(len(mc)):
x1, x2 = gmm.gauss_ellipse_2d(centroids[i], ccov[i])
plot(x1, x2, 'k', linewidth=2)
xlabel('$x_1$'); ylabel('$x_2$')
The resulting plot should look something like this:
The probability denisity function (PDF) can be evaluated using the following function:
Gaussian Mixture Models
- pypr.clustering.gmm.gmm_pdf(X, centroids, ccov, mc, individual=False)¶
Evaluates the PDF for the multivariate Guassian mixture.
Draw samples from a Mixture of Gaussians (MoG)
Parameters : centroids : list
List of cluster centers - [ [x1,y1,..],..,[xN, yN,..] ]
ccov : list
List of cluster co-variances DxD matrices
mc : list
- Mixing cofficients for each cluster (must sum to one)
by default equal for each cluster.
individual : bool
If True the probability density is returned for each cluster component.
Returns : prob : 1d np array
Probability density values for entries in X.
For more information mixture models and expectation maximization take a look at Pattern Recognition and Machine Learning by Christopher M. Bishop [bishop2006].
| [wikimixmodel] | Mixture model. (2010, December 23). In Wikipedia, The Free Encyclopedia. Retrieved 12:33, February 25, 2011, from http://en.wikipedia.org/w/index.php?title=Mixture_model&oldid=403871987 |
| [bishop2006] | (1, 2, 3) Pattern Recognition and Machine Learning, Christopher M. Bishop, Springer (2006) |
Expectation Maximization¶
In the previous example we saw how we could draw samples from a Gaussian Mixture Model.
Now we will look at how we can work in the opposite direction, given a set of samples find a set of K multivariate Gaussian
distributions that represent observed samples in a good way.
The number of clusters, 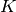 , is given, so the parameters that are to be found are the means and covariances of the distributions.
, is given, so the parameters that are to be found are the means and covariances of the distributions.
An acknowledged and efficient method for finding the parameters of a GMM is to use Expectation Maximization (EM). The EM algorithm is an iterative refinement algorithm used for finding maximum likelihood estimates of parameters in probabilistic models. The likelihood is a measure for how good the data fits a given model, and is a function of the parameters of the statistical model. If we assume that all the samples in the dataset are independent, then we can write the likelihood as,

and as we are using a mixture of gaussians as model, we can write

In contrast to the K-means algorithm, the EM algorithm for Gaussian Mixture does not assign each sample to only one cluster.
Instead, it assigns each sample a set of weights representing the sample’s probability of membership to each cluster.
This can be expressed with a conditional probability,  , given a sample
, given a sample 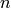 gives the probability of the sample being drawn a certain cluster
gives the probability of the sample being drawn a certain cluster 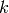 .
A responsibility matrix
.
A responsibility matrix  with elements
with elements  is used to hold the probabilities.
is used to hold the probabilities.

Given the data and the model parameters  ,
,  , and
, and  , we now can calculate the likeliness
, we now can calculate the likeliness  and the probabilities
and the probabilities  .
This is the expectation (E) step in EM-algorithm.
.
This is the expectation (E) step in EM-algorithm.
In the maximization (M) step we estimate the mean, co-variances, and mixing coefficients  .
As each point has a probability of belonging to a cluster,
.
As each point has a probability of belonging to a cluster,  , we have to weight each sample’s contribution to the paramter with that factor. The following equations are used to estimate the new set of model parameters.
, we have to weight each sample’s contribution to the paramter with that factor. The following equations are used to estimate the new set of model parameters.



The function pypr.clustering.gmm.em() is used to called to initialise and find the GMM. It will retry max_tries times if it encounters problems with the covariance matrix. The methods calls pypr.clustering.gmm_init() to initalized the clusters, and the keyword arguments passed to this can be specified using init_kw parameter.
It can be problematic to initalize the EM algorithm with the box initalization, as it might be numerically challenging calculating the log likelihood in the first step. Initalizing the EM algorithm with with either sample or kmeans should not pose any problems.
If you examine the code for the GMM EM algorithm, pypr.clustering.gmm.em(), you can see that the code uses the log-sum-exp formula cite{numericalrecipes} to avoid underflow in the floating point calculations.
Condtional and marginal distributions¶
The conditional and marginal distributions can be easily derived from the joint probability described by the GMM, see [bishop2006], [rasmussen2006], [sung2004].
Let  and
and  be jointly Gaussian vectors, and given a GMM with the Guassian distributions
be jointly Gaussian vectors, and given a GMM with the Guassian distributions  with
with 


Then the marginal distribution can be written as

and the conditional distribution for each Gaussian component 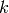 is given by
is given by


and for the whole GMM as

It is also possible to use a mixture of gaussians for regression.
This is done by using the conditional distribution, so that we have  .
When using the GMM for regression, the model output can be calculated as the expected value of the conditional GMM probability density function
.
When using the GMM for regression, the model output can be calculated as the expected value of the conditional GMM probability density function

Here is an example which uses EM to find the the parameters for the Gaussian Mixture Model (GMM), and then plots the conditional distribution for one of the parameters.
# An example of using the Expectation Maximization (EM) algorithm to find the
# parameters for a mixture of gaussian given a set of samples.
from numpy import *
from matplotlib.pylab import *
import pypr.clustering.gmm as gmm
def iter_plot(cen_lst, cov_lst, itr):
# For plotting EM progress
if itr % 2 == 0:
for i in range(len(cen_lst)):
x,y = gmm.gauss_ellipse_2d(cen_lst[i], cov_lst[i])
plot(x, y, 'k', linewidth=0.5)
seed(1)
mc = [0.4, 0.4, 0.2] # Mixing coefficients
centroids = [ array([0,0]), array([3,3]), array([0,4]) ]
ccov = [ array([[1,0.4],[0.4,1]]), diag((1,2)), diag((0.4,0.1)) ]
# Generate samples from the gaussian mixture model
X = gmm.sample_gaussian_mixture(centroids, ccov, mc, samples=1000)
fig1 = figure()
plot(X[:,0], X[:,1], '.')
# Expectation-Maximization of Mixture of Gaussians
cen_lst, cov_lst, p_k, logL = gmm.em_gm(X, K = 3, iter = 400,\
verbose = True, iter_call = iter_plot)
print "Log likelihood (how well the data fits the model) = ", logL
# Plot the cluster ellipses
for i in range(len(cen_lst)):
x1,x2 = gmm.gauss_ellipse_2d(cen_lst[i], cov_lst[i])
plot(x1, x2, 'k', linewidth=2)
title(""); xlabel(r'$x_1$'); ylabel(r'$x_2$')
# Now we will find the conditional distribution of x given y
fig2 = figure()
ax1 = subplot(111)
plot(X[:,0], X[:,1], ',')
y = -1.0
axhline(y)
x1plt = np.linspace(axis()[0], axis()[1], 200)
for i in range(len(cen_lst)):
text(cen_lst[i][0], cen_lst[i][1], str(i+1), horizontalalignment='center',
verticalalignment='center', size=32, color=(0.2,0,0))
ex,ey = gmm.gauss_ellipse_2d(cen_lst[i], cov_lst[i])
plot(ex, ey, 'k', linewidth=0.5)
ax2 = twinx()
(con_cen, con_cov, new_p_k) = gmm.cond_dist(np.array([np.nan, y]), \
cen_lst, cov_lst, p_k)
x2plt = gmm.gmm_pdf(c_[x1plt], con_cen, con_cov, new_p_k)
ax2.plot(x1plt, x2plt,'r', linewidth=2,
label='Cond. dist. of $x_1$ given $x_2='+str(y)+'$')
ax2.legend()
ax1.set_xlabel(r'$x_1$')
ax1.set_ylabel(r'$x_2$')
ax2.set_ylabel('Probability')
The resulting plot should look something similar to this:

| [sung2004] | Gaussian Mixture Regression and Classiufb01cation, H. G. Sung, Rice University (2004) |
| [rasmussen2006] | Gaussian Processes for Machine Learning, Carl Edward Rasmussen and Christopher K. I. Williams, MIT Press (2006) |
Application Programming Interface¶
Gaussian Mixture Models
- exception pypr.clustering.gmm.Cov_problem¶
- pypr.clustering.gmm.cond_dist(Y, centroids, ccov, mc)¶
Finds the conditional distribution p(X|Y) for a GMM.
Parameters : Y : NxD array
An array of inputs. Inputs set to NaN are not set, and become inputs to the resulting distribution. Order is preserved.
centroids : list
List of cluster centers - [ [x1,y1,..],..,[xN, yN,..] ]
ccov : list
List of cluster co-variances DxD matrices
mc : list
Mixing cofficients for each cluster (must sum to one) by default equal for each cluster.
Returns : res : tuple
A tuple containing a new set of (centroids, ccov, mc) for the conditional distribution.
- pypr.clustering.gmm.em(X, K, max_iter=50, verbose=False, iter_call=None, delta_stop=9.9999999999999995e-07, init_kw={}, max_tries=10, diag_add=0.001)¶
Find K cluster centers in X using Expectation Maximization of Gaussian Mixtures.
Parameters : X : NxD array
Input data. Should contain N samples row wise, and D variablescolumn wise.
max_iter : int
Maximum allowed number of iterations/try.
iter_call : callable
Called for each iteration: iter_call(center_list, cov_list, p_k, i)
delta_stop : float
Stop when the change in the mean negative log likelihood goes below this value.
max_tries : int
The co-variance matrix for some cluster migth end up with NaN values, then the algorithm will restart; max_tries is the number of allowed retries.
diag_add : float
A scalar multiplied by the variance of each feature of the input data, and added to the diagonal of the covariance matrix at each iteration.
Centroid initialization is given by *cluster_init*, the only available options :
are ‘sample’ and ‘kmeans’. ‘sample’ selects random samples as centroids. ‘kmeans’ :
calls kmeans to find the cluster centers. :
Returns : center_list : list
A K-length list of cluster centers
cov_list : list
A K-length list of co-variance matrices
p_k : list
An K length array with mixing cofficients (p_k)
logLL : list
Log likelihood (how well the data fits the model)
- pypr.clustering.gmm.em_gm(X, K, max_iter=50, verbose=False, iter_call=None, delta_stop=9.9999999999999995e-07, init_kw={}, max_tries=10, diag_add=0.001)¶
Find K cluster centers in X using Expectation Maximization of Gaussian Mixtures.
Parameters : X : NxD array
Input data. Should contain N samples row wise, and D variablescolumn wise.
max_iter : int
Maximum allowed number of iterations/try.
iter_call : callable
Called for each iteration: iter_call(center_list, cov_list, p_k, i)
delta_stop : float
Stop when the change in the mean negative log likelihood goes below this value.
max_tries : int
The co-variance matrix for some cluster migth end up with NaN values, then the algorithm will restart; max_tries is the number of allowed retries.
diag_add : float
A scalar multiplied by the variance of each feature of the input data, and added to the diagonal of the covariance matrix at each iteration.
Centroid initialization is given by *cluster_init*, the only available options :
are ‘sample’ and ‘kmeans’. ‘sample’ selects random samples as centroids. ‘kmeans’ :
calls kmeans to find the cluster centers. :
Returns : center_list : list
A K-length list of cluster centers
cov_list : list
A K-length list of co-variance matrices
p_k : list
An K length array with mixing cofficients (p_k)
logLL : list
Log likelihood (how well the data fits the model)
- pypr.clustering.gmm.find_density_diff(center_list, cov_list, p_k=None, method='hellinger')¶
Difference measures for each component of the GMM.
Parameters : centroids : list
List of cluster centers - [ [x1,y1,..],..,[xN, yN,..] ]
ccov : list
List of cluster co-variances DxD matrices
p_k : list
Mixing cofficients for each cluster (must sum to one) by default equal for each cluster.
method : string, optional
Select difference measure to use. Can be:
- ‘hellinger’ :
- ‘hellinger_weighted’ :
- ‘KL’ : Kullback-Leibler divergence
Returns : diff : NxN np array
The difference between the probability distribtions of the components pairwise. Only the upper triangular matrix is used.
- pypr.clustering.gmm.gauss_ellipse_2d(centroid, ccov, sdwidth=1, points=100)¶
Returns x,y vectors corresponding to ellipsoid at standard deviation sdwidth.
- pypr.clustering.gmm.gm_assign_to_cluster(X, center_list, cov_list, p_k)¶
Assigns each sample to one of the Gaussian clusters given.
Returns an array with numbers, 0 corresponding to the first cluster in the cluster list.
- pypr.clustering.gmm.gm_log_likelihood(X, center_list, cov_list, p_k)¶
Finds the likelihood for a set of samples belongin to a Gaussian mixture model.
Return log likelighood
- pypr.clustering.gmm.gmm_em_continue(X, center_list, cov_list, p_k, max_iter=50, verbose=False, iter_call=None, delta_stop=9.9999999999999995e-07, diag_add=0.001, delta_stop_count_end=10)¶
- pypr.clustering.gmm.gmm_init(X, K, verbose=False, cluster_init='sample', cluster_init_prop={}, max_init_iter=5, cov_init='var')¶
Initialize a Gaussian Mixture Model (GMM). Generates a set of inital parameters for the GMM.
Returns : center_list : list
A K-length list of cluster centers
cov_list : list
A K-length list of co-variance matrices
p_k : list
An K length array with mixing cofficients
- pypr.clustering.gmm.gmm_pdf(X, centroids, ccov, mc, individual=False)
Evaluates the PDF for the multivariate Guassian mixture.
Draw samples from a Mixture of Gaussians (MoG)
Parameters : centroids : list
List of cluster centers - [ [x1,y1,..],..,[xN, yN,..] ]
ccov : list
List of cluster co-variances DxD matrices
mc : list
- Mixing cofficients for each cluster (must sum to one)
by default equal for each cluster.
individual : bool
If True the probability density is returned for each cluster component.
Returns : prob : 1d np array
Probability density values for entries in X.
- pypr.clustering.gmm.logmulnormpdf(X, MU, SIGMA)¶
Evaluates natural log of the PDF for the multivariate Guassian distribution.
Parameters : X : np array
Inputs/entries row-wise. Can also be a 1-d array if only a single point is evaluated.
MU : nparray
Center/mean, 1d array.
SIGMA : 2d np array
Covariance matrix.
Returns : prob : 1d np array
Log (natural) probabilities for entries in X.
- pypr.clustering.gmm.marg_dist(X_idx, centroids, ccov, mc)¶
Finds the marginal distribution p(X) for a GMM.
Parameters : X_idx : list
Indecies of dimensions to keep
centroids : list
List of cluster centers - [ [x1,y1,..],..,[xN, yN,..] ]
ccov : list
List of cluster co-variances DxD matrices
mc : list
Mixing cofficients for each cluster (must sum to one) by default equal for each cluster.
Returns : res : tuple
A tuple containing a new set of (centroids, ccov, mc) for the marginal distribution.
- pypr.clustering.gmm.mulnormpdf(X, MU, SIGMA)¶
Evaluates the PDF for the multivariate Guassian distribution.
Parameters : X : np array
Inputs/entries row-wise. Can also be a 1-d array if only a single point is evaluated.
MU : nparray
Center/mean, 1d array.
SIGMA : 2d np array
Covariance matrix.
Returns : prob : 1d np array
Probabilities for entries in X.
Examples
from pypr.clustering import * from numpy import * X = array([[0,0],[1,1]]) MU = array([0,0]) SIGMA = diag((1,1)) gmm.mulnormpdf(X, MU, SIGMA)
- pypr.clustering.gmm.predict(X, centroids, ccov, mc)¶
Predict the entries in X, which contains NaNs.
Parameters : X : np array
2d np array containing the inputs. Target are specified with numpy NaNs. The NaNs will be replaced with the most probable result according to the GMM model provided.
centroids : list
List of cluster centers - [ [x1,y1,..],..,[xN, yN,..] ]
ccov : list
List of cluster co-variances DxD matrices
mc : list
Mixing cofficients for each cluster (must sum to one) by default equal for each cluster.
Returns : Nothing - X is modified :
- pypr.clustering.gmm.sample_gaussian_mixture(centroids, ccov, mc=None, samples=1)
Draw samples from a Mixture of Gaussians (MoG)
Parameters : centroids : list
List of cluster centers - [ [x1,y1,..],..,[xN, yN,..] ]
ccov : list
List of cluster co-variances DxD matrices
mc : list
- Mixing cofficients for each cluster (must sum to one)
by default equal for each cluster.
Returns : X : 2d np array
A matrix with samples rows, and input dimension columns.
Examples
from pypr.clustering import * from numpy import * centroids=[array([10,10])] ccov=[array([[1,0],[0,1]])] samples = 10 gmm.sample_gaussian_mixture(centroids, ccov, samples=samples)