Artificial Neural Network¶
This section gives an introduction to the Artificial Neural Network implemented in PyPR. The implmented ANN supports several network outputs and efficient evaluation of the error gradient using backpropagation.
An Artificial Neural Network can map serval inputs to several outputs
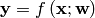
where 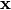 and
and 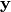 are a vectors with inputs and output values respectivily.
The function
are a vectors with inputs and output values respectivily.
The function 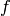 is consistst of mathematical function for the neural network, which can be controlled by a set of parmeters
is consistst of mathematical function for the neural network, which can be controlled by a set of parmeters 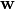 .
In the context of ANN these parameters are most commonly called weights.
The weight can be adjusted to get the desired mapping from
.
In the context of ANN these parameters are most commonly called weights.
The weight can be adjusted to get the desired mapping from 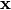 , this process is called the training of the network.
, this process is called the training of the network.
Network Structure and Evaluation¶
The feedforward network structure supported by the PyPR.
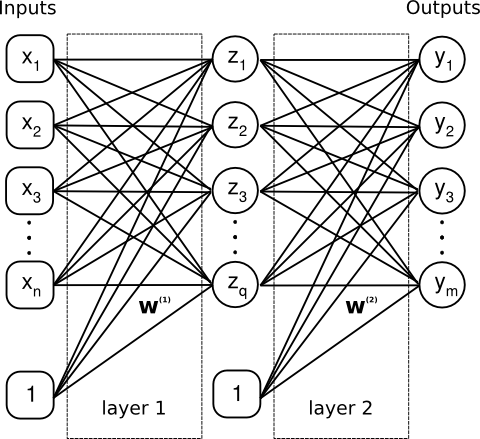
A 2-layer feedforward artifical neural network.
The figure 2 layer feedforward ANN shows a typical 2-layer feedforward artifical neural network. On the left side of the network the inputs are given, and on the right the outputs. The network is called a feed forward because the data only moves in one direction; from the input towards the outputs. The nodes drawn as circles are called perceptrons. They sum all their inputs, and apply a activtion function. The perceptrons will be investigated shortly. The figure 2 layer feedforward ANN is for a two layer network, but the network can consist of fewer of more layers. The 2-layer network will be used here for explaining the basic concepts of the ANN. A bias node is also located together with the inputs, and is supplied by the network itself. It always gives a value of one, and helps the network handle zero only inputs better.
The lines denote the adjustable weights  .
A weight matrix is given for each layer. A layer’s weight matrix is identified by a superscript number
.
A weight matrix is given for each layer. A layer’s weight matrix is identified by a superscript number 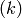 ,
, 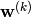 , where
, where 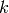 is the layer number.
Each element in the weight matrix
is the layer number.
Each element in the weight matrix 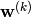 is denoted
is denoted 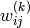 , which is the weight value for the connection from node
, which is the weight value for the connection from node 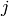 to node
to node 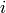 .
.
To find the an output of the network, the inputs are passed forward through the network.
Let us first find the outputs of the first layer of perceptrons.
A more detailed drawing of the node or perceptron 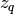 could look like this:
could look like this:
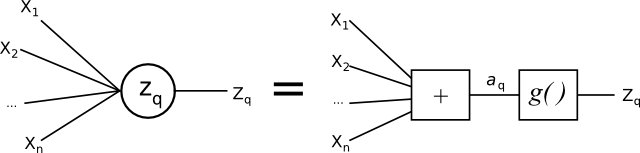
A perceptron.
The total input to the perceptron 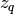 is given by
is given by
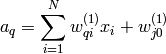
where 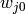 is the weight that has been assigned the bias unit.
If we also assign
is the weight that has been assigned the bias unit.
If we also assign 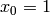 , the equation can be simplified to
, the equation can be simplified to
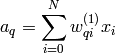
The output of the hidden perceptron 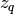 is found by applying its activation function,
is found by applying its activation function, 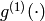 , to the nodes total input,
, to the nodes total input, 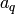 :
:
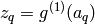
The second layer of perceptrons is handled in a similar manner, and the output from the network can be written as
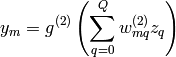
By inserting the expression for 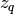 we get the full expression for a 2-layer ANN
we get the full expression for a 2-layer ANN
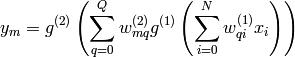
About the activation function.

In the ANN implementation there is a matrix for each layer with the weights. The last column in the weight matrix gives the weights assigned to the bias node from the previous layer.
Examining the Weight Matrix Structure¶
The weight matrices used in PyPR have the bias weights added as the last column.
Here is an example of createing a ANN with PyPR:
>>> import pypr.ann as ann
>>> nn = ann.ANN([1,3,1]) # A network with 1 inputs, 3 hidden nodes, and 1 output
>>> nn.weights[0] # First layer of weights W^(1)
array([[ 2.45579029, -2.22287964],
[-1.75201183, 0.05098648],
[ 0.95317093, 0.84703608]])
>>> nn.weights[1] # Second layer of weights W^(2)
array([[-0.54627072, -0.67273706, 1.42473486, -0.21274268]])
The create ANN has 1 input, 3 hidden nodes, and 1 output. The example show how to obtain the weight matrices. The first matrix is 3x2. The first column is for the input, and the last for the bias node. The rows give the weight to each unit in the hidden layer next.
The second weight matrix is 1x4. All the outputs from the hidden layer go to 1 output perceptron. The last column here again is due to the bias node.
Training¶
The NN need data to be trained. For this purpose the is a special container class, which handles the joins the training data and the NN.
Purpose of error function
Activation and Error Functions¶
The activation functions are implemented in pypr.ann.activation_functions. The are implemented as 2-tuples. The first element is a reference to the activation function, and the second a reference to its derivative with regard to the input value.
| Name | Function | Derivative |
|---|---|---|
| Linear |  |
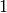 |
| Sigmoid | 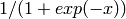 |
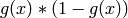 |
| Tanh | 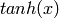 |
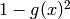 |
The value passed to derivative method is actually 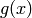 , and not
, and not  .
One should only be aware of this, if implementing new activation functions.
.
One should only be aware of this, if implementing new activation functions.
Here is a toy example where we assign all three activation functions:
import pypr.ann as ann
import pypr.ann.activation_functions as af
nn = ann.WeightDecayANN([1,1,1,1], [af.tanh, af.sigmoid, af.lin]))
TODO: Selecting activation and error functions.
Classification¶
A neural network can be trained to find the posterior probabilities, which reflects the uncertainty that a sample belongs to a given set of classes.
A general case of classification, is when the observations have to be classified into 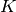 classes.
The ANN will have
classes.
The ANN will have 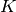 outputs, one for each class.
If the observation belongs to a class
outputs, one for each class.
If the observation belongs to a class 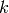 the corresponding output number will be 1, otherwise the outputs are 0.
This is called a 1-of-K binary coding scheme.
the corresponding output number will be 1, otherwise the outputs are 0.
This is called a 1-of-K binary coding scheme.
If the output of the network should be considered as probabilities, they have to fulfill some requirements, which are 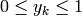 and
and
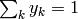 .
.
This can be achieved using the softmax activation function
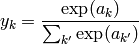
According to [bishop95] the conditional distribution for this setup can be written as
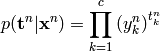
and the negative log likelihood function of the cross entropy can be expressed as
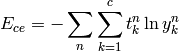
Attention
The entropic cost function and softmax activation function must be used together due to the implementation. If the entropic cost function is used, then the softmax activation function must be used on the output layer. And the softmax activation function can only be used in this layer.
Multiclass classification using ANN gives a classification example of the well-known Iris dataset using the softmax activation function and cross entropy error function.
Implementation overview¶
The ANN is implemented in a class called ANN and extended by WeightDecayANN, which adds weight decay support. This is done by modifying the gradient and error functions accordingly.
The ANN class can flatten the weights in all the layer into a vector. This is handy, because then general purpose function minimization can be used for training the ANN.
| [elliott] | Technical Research Report, A Better Activation Function for Artificial Neural Networks, D.L. Elliott, University of Maryland, 1993 |
| [bishop95] | Neural Networks for Pattern Recognition, Christopher M. Bishop, Oxford University Press, 1995 |
| [bishop06] | Pattern Recognition and Machine Learning, Christopher M. Bishop, Springer, 2006 |
Application Programming Interface¶
- class pypr.ann.ann.ANN(nodes, afunc=[], errorfunc=None)¶
A simple implementation of a feed forward neural network.
Methods
- find_flat_weight_no(layerNo, r, c)¶
Returns the corresponding flat weight index to layer and weight index. This is not very fast, so do not use it for anything but small examples or testing.
- find_weight(flatWno)¶
Parameters : flatWno : int
The number of the weight in a flattened vector
Returns : pos : tuple
Returns the layer number, row, and column where weight is found - (layer, r, c)
This is not very fast, so do not use it for anything but small :
examples or testing. :
- forward(inputs)¶
Returns the output from the output layer.
Parameters : inputs : NxD np array
An array with N samples with D dimensions (features). For example an input with 2 samples and 3 dimensions:
- inputs = array([[1,2,3],
[3,4,5]])
Returns : result : np array
A NxD’ array, where D’ is the number of outputs of the network.
- forward_get_all(inputs)¶
Returns the outputs from all layers, from input to output.
Parameters : inputs : NxD np array
An array with N samples with D dimensions (features). For example an input with 2 samples and 3 dimensions:
- inputs = array([[1,2,3],
[3,4,5]])
Returns : result : list
A list of 2d np arrays. The all the arrays will have N rows, the number of outputs for each array will depend on the of nodes in that particular layer.
- get_af_summed_weighs()¶
Returns : sum : scalar
Returns the sum of all the weights to the input of a note’s activation function.
- get_base_error_func()¶
Returns : error_func : function
This is the error function which back propagation uses. Should normally not be overwritten. This error function does not include the weight decay.
- get_error_func()¶
Returns : error_func : function
The error function. This function can be overwritten, so for example a network with weight decay will return the error function with the weight decay penality.
- get_flat_weight(flatWno)¶
Returns the value of the weight corresponding to flat weight index.
- get_flat_weights()¶
Returns : W : 1d np array
Returns all the weights of the network in a vector form. From input to output layer. This is useful for the optimization methods, which normally only operate on an 1d array.
- get_num_layers()¶
Returns : Nw : int
Number of weights layers in the network.
- get_weight_copy()¶
Returns : weights : list
Copy of the current weights. The length of the list is equal to the number of hidden layers.
- gradient(inputs, targets, errorfunc=None)¶
Calculate the derivatives of the error function. Return a matrix corresponding to each weight matrix.
Parameters : inputs : NxD np array
The inputs are given as, N, rows, with D features/dimensions.
targets : NxT np array
The N targets corresponding to the inputs. The number of outputs is given by T.
Returns : gradient : list
List of gradient matrices.
- gradient_descent_train(inputs, targets, eta=0.001, maxitr=20000)¶
Train the network using the gradient descent method. This method shouldn’t relly be used. Use the more advanced methods.
Parameters : inputs : NxD np array
The inputs are given as, N, rows, with D features/dimensions.
targets : NxT np array
The N targets corresponding to the inputs. The number of outputs is given by T.
For example one could use the XOR function as an example: :
- inputs = array([[0,0],
[0,1], [1,0], [1,1]])
targets = array([[0],[1],[1],[0]])
- set_flat_weight(flatWno, value)¶
Sets the value of the weight with flat weight index.
- set_flat_weights(W)¶
Set the weights of the network according to a vector of weights.
Parameters : W : 1d np array
W must have the correct length, otherwise it will not work.
- class pypr.ann.ann.WeightDecayANN(*args, **kwargs)¶
This modifies the error function and the gradient to accommodate weight decay, otherwise it works just like an ANN.
Methods
error_with_weight_penalty find_flat_weight_no find_weight forward forward_get_all get_af_summed_weighs get_base_error_func get_error_func get_flat_weight get_flat_weights get_num_layers get_weight_copy gradient gradient_descent_train set_flat_weight set_flat_weights - get_error_func()¶
Returns a modified error function with a weight decay penalty.
Activation functions¶
Error functions¶
An error function is represented as a tuple with a function for evaluating networks error and its derivatives.