Gaussian Process¶
A Gaussian process is defined by its mean and covariance functions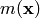 
and 
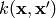respectivily
![\begin{array}{c}
m(\mathbf{x}) = \mathbb{E} \left [ f(\mathbf{x}) \right ], \\
k(\mathbf{x},\mathbf{x}') = \mathbb{E} \left [
\left ( f(\mathbf{x})-m(\mathbf{x})\right )
\left ( f(\mathbf{x}')-m(\mathbf{x}')\right )
\right ]
\end{array}](_images/math/ee4c074dfbe9121f51938360f5d9813b189135cf.png)
and Gaussian Process (GP) can be written as
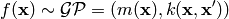
The free parameters in the covariance functions are called hyperparameters.
Regression¶
When doing regression we are interested in finding the model outputs for a given set of inputs, and the confidence of the predictions. We have training dataset
![\left [
\begin{array}{c}
\mathbf{f} \\ \mathbf{f_{*}}
\end{array}
\right ]
\sim
\mathcal{N}
\left (
0,
\left [
\begin{array}{cc}
K(X,X) & K(X,X_{*}) \\
K(X_{*},X) & K(X_{*},X_{*}) \\
\end{array}
\right ]
\right )
\sim
\mathcal{N}
\left (
0,
\left [
\begin{array}{cc}
K & K_{*}^T \\
K_{*} & K_{{*}{*}} \\
\end{array}
\right ]
\right )](_images/math/9b430c93eeed031d7bbbbcf8bdf99103132ba303.png)
For simplicity we have set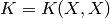 
, 
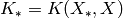, and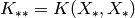 
.
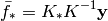
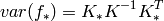
Finding the hyper-parameters¶
Application Programming Interface¶
- class pypr.gp.GaussianProcess.GPR(GP, X, y, max_itr=200, callback=None, print_progress=False, no_train=False, mean_tol=None)¶
Gaussian Process for regression.
Methods
df f find_hyperparameters predict - df(params=None)¶
The partial derivatives of the function to minimize, which is the likihood in this case. This method is passed to the optimizer.
Parameters : params : 1D np array, optional
hyper-parameters to evaluate at. It not specified, then the current values in the covariance function are used.
Returns : der : np array
array of partial derivatives
- f(params=None)¶
The function to minimize, which is the likihood in this case. This method is passed to the optimizer.
Parameters : params : 1D np array, optional
hyper-parameters to evaluate at. It not specified, then the current values in the covariance function are used.
Returns : nllikelihood : float
Negative log likihood
- find_hyperparameters(max_itr=None)¶
Find hyperparameters for the GP.
- predict(XX)¶
Predict the the output of the GPR for the inputs given in XX
Parameters : XX : NxD np array
An array containing N samples, with D inputs
Returns : res : np array
An array of length N containing the outputs of the network
- class pypr.gp.GaussianProcess.GaussianProcess(cf)¶
Gaussian Process class.
Methods
find_likelihood_der fit_data generate regression - find_likelihood_der(X, y)¶
Find the negative log likelihood and its partial derivatives.
- fit_data(X, y)¶
Fit the hyper-parameters to the data.
X Input samples (2d array, samples row-wise) y Function output (1d array)
- generate(x, rn=None)¶
Generate samples from the GP.
Parameters : x : np array
A 2d matrix with samples row-wise
rn : np array
Provide your own random numbers (mostly just for testing)
- regression(X, y, XX, max_samples=1000)¶
Predict the y values for XX given the X, y, and the objects covariance function.
Parameters : X : MxD np array
training array containing M samples of dimension D
y : 1-dimensional np array of length M
training outputs
XX : NxD np array
An array containing N samples, with D inputs
max_samples : int, optional
Due to memory considerations, the inputs are evaluated part at a time. The maximum number of samples evaluated in each interation is given by max_samples
Returns : ys : np array of length N
output of GPR
s2 : np array of length N
corresponding variance