Statistic and Statistical Tests¶
Bayesian Information Criterion¶
When estimating model parameters using maximum likelihood estimation, it is possible to increase the likelihood by adding parameters, which may result in overfitting. The BIC resolves this problem by introducing a penalty term for the number of parameters in the model. This penalty is larger in the BIC than in the related AIC. [wikibic].
A rough approximation [bisp2006] [calinon2007] of the Bayesian Information Criterion (BIC) is given by
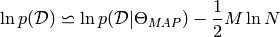
where 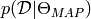 is the likelihood of the data given model, and
is the likelihood of the data given model, and 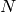 is the number of samples, and
is the number of samples, and 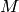 is the number of free parameters
is the number of free parameters 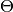 in the model (omitted in equation for simplicity).
in the model (omitted in equation for simplicity).
The number of free parameters is given by the model used.
The number of parameters in a Gaussian Mixture Model (GMM) with 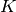 clusters and a full covariance matrix, can be found by counting the free parameters in the means and covariances, which should give [calinon2007]
clusters and a full covariance matrix, can be found by counting the free parameters in the means and covariances, which should give [calinon2007]
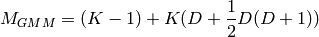
the parameter 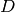 specifies the number of dimensions.
specifies the number of dimensions.
There is an example Finding the Number of Clusters to use in a Gaussian Mixture Model that gives an example of using the BIC for controlling the complexity of a Gaussian Mixture Model (GMM). The example generates a plot, which should look something like this:

| [bisp2006] | Christopher M. Bishop. Pattern Recognition and Machine Learning (Infor- mation Science and Statistics). Springer-Verlag New York, Inc., Secaucus, NJ, USA, 2006. |
| [calinon2007] | (1, 2) Sylvain Calinon, Florent Guenter, and Aude Billard. On learning, repre- senting, and generalizing a task in a humanoid robot. Systems, Man and Cybernetics, Part B, IEEE Transactions on, 37(2):286-298, 2007. http://programming-by-demonstration.org/papers/Calinon-JSMC2007.pdf |
| [wikibic] | Bayesian information criterion. (2011, February 21). In Wikipedia, The Free Encyclopedia. Retrieved 11:57, March 1, 2011, from http://en.wikipedia.org/w/index.php?title=Bayesian_information_criterion&oldid=415136150 |
Akaike Information Criterion¶
To be done.
Sample Autocorrelation¶
Supposed we have a time series given by 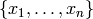 with
with 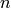 samples.
The sample autocorrelation is calculated as follows:
samples.
The sample autocorrelation is calculated as follows:
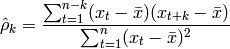
where 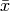 is the mean for
is the mean for 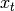 , and
, and 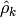 is the sample autocorrelation
is the sample autocorrelation
- pypr.stattest.ljungbox.sac(x, k=1)¶
Sample autocorrelation (As used in statistics with normalization)
http://en.wikipedia.org/wiki/Autocorrelation
Parameters : x : 1d numpy array
Signal
k : int or list of ints
Lags to calculate sample autocorrelation for
Returns : res : scalar or np array
The sample autocorrelation. A scalar value if k is a scalar, and a numpy array if k is a interable.
Ljung-Box Test¶
The Ljung-Box test is a type of statistical test of whether any of a group of autocorrelations of a time series are different from zero. Instead of testing randomness at each distinct lag, it tests the “overall” randomness based on a number of lags [wikiljungbox].
The test statistic is:
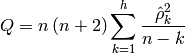
where 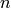 is the sample size,
is the sample size, 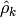 is the sample autocorrelation at lag
is the sample autocorrelation at lag 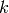 , and
, and 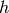 is the number of lags being tested [wikiljungbox]. This function is implemented in:
is the number of lags being tested [wikiljungbox]. This function is implemented in:
- pypr.stattest.ljungbox.ljungbox(x, lags, alpha=0.10000000000000001)¶
The Ljung-Box test for determining if the data is independently distributed.
Parameters : x : 1d numpy array
Signal to test
lags : int
Number of lags being tested
Returns : Q : float
Test statistic
For significance level 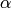 , the critical region for rejection of the hypothesis of randomness is [wikiljungbox].
, the critical region for rejection of the hypothesis of randomness is [wikiljungbox].
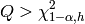
where 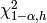 is the
is the 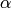 -quantile of the chi-square distribution with
-quantile of the chi-square distribution with 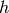 degrees of freedom.
The chi-square distribution can be found in scipy.stats.chi2.
degrees of freedom.
The chi-square distribution can be found in scipy.stats.chi2.
Example¶
This example uses the sample autocorrelation, acf(...), which also is defined in pypr.stattest module.
from pypr.stattest.ljungbox import *
import scipy.stats
x = np.random.randn(100)
#rg = genfromtxt('sunspots/sp.dat')
#x = rg[:,1] # Just use number of sun spots, ignore year
h = 20 # Number of lags
lags = range(h)
sa = np.zeros((h))
for k in range(len(lags)):
sa[k] = sac(x, k)
figure()
markerline, stemlines, baseline = stem(lags, sa)
grid()
title('Sample Autocorrealtion Function (ACF)')
ylabel('Sample Autocorrelation')
xlabel('Lag')
h, pV, Q, cV = lbqtest(x, range(1, 20), alpha=0.1)
print 'lag p-value Q c-value rejectH0'
for i in range(len(h)):
print "%-2d %10.3f %10.3f %10.3f %s" % (i+1, pV[i], Q[i], cV[i], str(h[i]))
The example generates a sample autocorrelation for the sun spot data set, and calculates the Ljung-Box test statistics.

The output should look something similar to this:
lag p-value Q c-value rejectH0
1 0.164 1.935 2.706 False
2 0.378 1.948 4.605 False
3 0.542 2.148 6.251 False
4 0.600 2.752 7.779 False
5 0.718 2.884 9.236 False
6 0.823 2.884 10.645 False
7 0.895 2.885 12.017 False
8 0.941 2.897 13.362 False
9 0.966 2.948 14.684 False
10 0.941 4.132 15.987 False
11 0.888 5.781 17.275 False
12 0.922 5.887 18.549 False
13 0.724 9.625 19.812 False
14 0.744 10.242 21.064 False
15 0.756 10.949 22.307 False
16 0.746 11.969 23.542 False
17 0.801 11.979 24.769 False
18 0.847 12.008 25.989 False
19 0.885 12.020 27.204 False
| [wikiljungbox] | (1, 2, 3) Ljung–Box test. (2011, February 17). In Wikipedia, The Free Encyclopedia. Retrieved 12:46, February 23, 2011, from http://en.wikipedia.org/w/index.php?title=Ljung%E2%80%93Box_test&oldid=414387240 |
| [adres1766] | http://adorio-research.org/wordpress/?p=1766 |
| [mathworks-lbqtest] | http://www.mathworks.com/help/toolbox/econ/lbqtest.html |
Box-Pierce Test¶
The Ljung–Box test that we have just looked at is a preferred version of the Box–Pierce test, because the Box–Pierce statistic has poor performance in small samples [wikilboxpierce].
The test statistic is [cromwell1994]:
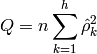
The implementation of the Box-Pierce is incorporated into the Ljung-Box code, and can be used by setting the method argument, lbqtest(..., method='bp'), when calling the Ljung-Box test.
| [wikilboxpierce] | Box–Pierce test. (2010, November 8). In Wikipedia, The Free Encyclopedia. Retrieved 15:52, February 24, 2011, from http://en.wikipedia.org/w/index.php?title=Box%E2%80%93Pierce_test&oldid=395462997 |
| [cromwell1994] | Univariate tests for time series models, Jeff B. Cromwell, Walter C. Labys, Michel Terraza, 1994 |
Application Programming Interface¶
- pypr.stattest.ljungbox.boxpierce(x, lags, alpha=0.10000000000000001)¶
The Box-Pierce test for determining if the data is independently distributed.
Parameters : x : 1d numpy array
Signal to test
lags : int
Number of lags being tested
Returns : Q : float
Test statistic
- pypr.stattest.ljungbox.lbqtest(x, lags, alpha=0.10000000000000001, method='lb')¶
The Ljung-Box test for determining if the data is independently distributed.
Parameters : x : 1d numpy array
Signal to test
lags : list of ints
Lags being tested
alpha : float
Significance level used for the tests
method : string
Can be either ‘lb’ for Ljung-Box, or ‘bp’ for Box-Pierce
Returns : h : np array
Numpy array of bool values, True == H0 hypothesis rejected
pV : np array
Test statistics p-values
Q : np array
Test statistics
cV : np array
Critical values used for determining if H0 should be rejected. The critical values are calculated from the given alpha and lag.
- pypr.stattest.ljungbox.ljungbox(x, lags, alpha=0.10000000000000001)
The Ljung-Box test for determining if the data is independently distributed.
Parameters : x : 1d numpy array
Signal to test
lags : int
Number of lags being tested
Returns : Q : float
Test statistic
- pypr.stattest.ljungbox.sac(x, k=1)
Sample autocorrelation (As used in statistics with normalization)
http://en.wikipedia.org/wiki/Autocorrelation
Parameters : x : 1d numpy array
Signal
k : int or list of ints
Lags to calculate sample autocorrelation for
Returns : res : scalar or np array
The sample autocorrelation. A scalar value if k is a scalar, and a numpy array if k is a interable.